Organização
Tipos de Programas
Visualização de dados
Introdução para variáveis
Matrizes e Vetores
Estruturas
Trabalhando com variáveis
Operadores
Instruções de comando
Rotinas de manipulação
Rotinas do ENVI
Matrizes e Vetores
Matricial e Vetorial
O IDL é uma linguagem baseada em matrizes sejam elas unidimensionais (vetores) ou bidimensionais.
Criação
| TIPO | FUNÇÃO DE CRIAÇÃO | ?NDICE QUE GERA A FUN??O |
Byte |
BYTARR |
BINDGEN |
Integer |
INTARR |
INDGEN |
Unsigned integer |
UINTARR |
UINDGEN |
Long integer |
LONARR |
LINDGEN |
Unsigned long integer |
ULONARR |
ULINDGEN |
64-bit integer |
LONG64ARR |
L64INDGEN |
Unsigned 64-bit integer |
ULONG64ARR |
UL64INDGEN |
Float |
FLTARR |
FINDGEN |
Double |
DBLARR |
DINDGEN |
Complex |
COMPLEXARR |
CINDGEN |
Double complex |
DCOMPLEXARR |
DCINDGEN |
String |
STRARR |
SINDGEN |
Pointer |
PTRARR |
|
Object |
OBJARR |
|
Undefined |
||
Structure |
REPLICATE |
Vetores e matrizes com diferentes tipos de variáveis e dados podem ser iniciados com rotinas do IDL como as listadas na tabela acima.
IDL> vec = fltarr (15)
IDL> vec[5] = 4.56
IDL> vec[13]= 1234.333
Matrizes e vetores no IDL começam com 0; consequentemente o vetor vec está subscrito de 0 até 14.
Vetores e matrizes também podem ser criados atribuindo à variável certo número de valores passados por colchetes.
IDL> temp = [12, 82, 97, 23, 0, 78]
Esta instrução cria um vetor de seis inteiros. Uma matriz de múltipla dimensão pode ser criada colocando valores dentro de vários colchetes dentro de dois colchetes, observe:
IDL> id4x4 = [ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1] ]
IDL> help, id4x4
ID4x4 INT = Array [4, 4]A variável id4x4 tornou-se uma matriz 4 X 4 de inteiros. Considere a instrução abaixo:
IDL> exemplo_arr = [3.4, 6.7D, 45U, 90L]
Esta instrução cria um vetor com diferentes tipos de variável. O IDL não apresenta problemas diante disso, ele executa uma conversão pelo tipo mais significativo. O tipo mais significativo nesta instrução é o double (6.7D). Todos os elementos do vetor são convertidos para double.
Operação de matrizes e vetores
Quando executamos uma operação com matrizes ou vetores no IDL, eles são executados em todos os elementos que estão dentro desta matriz ou vetor. Esta poderosa característica elimina a necessidade da utilização do laço para executar uma operação com cada um dos elementos.
IDL> x = findgen (360) * !dtor
IDL> sincurve = sin(x)
IDL> plot, sincurve
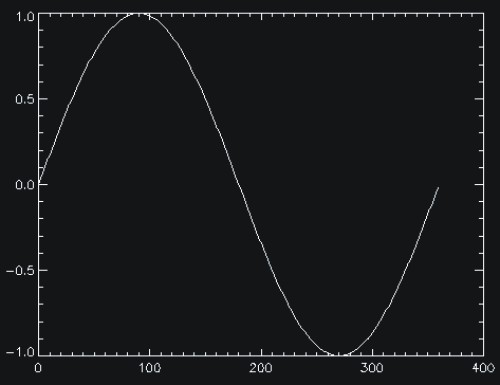
A primeira instrução multiplica os números 0.0, 1.0, 2.0, ....359.0 pela variável de sistemas !dtor fazendo a transformação de grau para radiano constante, então a segunda instrução calcula o seno de todos os elementos resultados pela transformação de graus em radianos, e a terceira linha de comando como já vimos anteriormente nesse manual exibe, um gráfico em linha do calculo final da matriz. Isto beneficia o IDL, eliminando o tempo consumido para controlar os laços, que executam as operações em todos os elementos do vetor. Use a vantagem desta possibilidade o máximo que poder - é mais rápido e mais fácil de ler.
Matrizes Multidimensionais
As matrizes no IDL podem ter até oito dimensões. No caso da matriz bidimensional do IDL a subscrição é especificada normalmente como [coluna, linha].
IDL> multi = lindgen (4, 6) ; quatro colunas, seis linhas
IDL> print, multi
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
O método de subscrição do IDL é por coluna. Internamente as matrizes são dispostas no formato de linha ( os elementos do multi são numerados na ordem em que eles são armazenados na memória). A subscrição em uma matriz bidimensional pode ser feita utilizando a notação [coluna, linha].
IDL> print, multi [1, 0], multi [3, 5]
1 23Todas as escalas de operadores podem ser utilizadas nas matrizes multidimensionais.
IDL> print, multi [*, 4] ; a quinta linha
16 17 18 19IDL> print, multi [2, *] ; a terceira coluna
2 |
6 |
10 |
14 |
18 |
22 |
IDL> print, multi [2: 3, 1: 2] ; uma quadra - a 3º e a 4º coluna e a 2º e 3º linha
6 7
10 11
Multiplicação de Matrizes
O operador # calcula o produto de uma matriz, multiplicando as colunas da primeira matriz pelas linhas da segunda. A segunda matriz deve ter o mesmo número de colunas que a primeira tem de linhas. A matriz resultante terá o número de colunas da primeira matriz e o mesmo número de linhas da segunda matriz.
Por exemplo:
IDL> a = indgen(3,2) ; matriz 3 X 2, na sintaxe do IDL.
IDL> print, a
0 1 2
3 4 5
IDL> b = indgen(2,3) ; matriz 2 X 3.
IDL> print, b
0 1
2 3
4 5
IDL> print, a # b
3 4 5
9 14 19
15 24 33Os cálculos são feitos desta forma:
A 0,0 . B 0,0 + A 0,1 . B 1,0 |
A 1,0 . B 0,0 + A 1,1 . B 1,0 |
A 2,0 . B 0,0 + A 2,1 . B 1,0 |
| A 0,0 . B 0,1 + A 0,1 . B 1,1 |
A 1,0 . B 0,1 + A 1,1 . B 1,1 |
A 2,0 . B 0,1 + A 2,1 . B 1,1 |
| A 0,0 . B 0,2 + A 0,1 . B 1,2 |
A 1,0 . B 0,2 + A 1,1 . B 1,2 |
A 2,0 . B 0,2 + A 2,1 . B 1, |
Usando os valores atuais:
( 0 ).( 0 ) + ( 3 ).( 1 ) |
( 1 ).( 0 ) + ( 4 ).( 1 ) |
( 2 ).( 0 ) + ( 5 ).( 1 ) |
| ( 0 ).( 2 ) + ( 3 ).( 3 ) |
( 1 ).( 2 ) + ( 4 ).( 3 ) |
( 2 ).( 2 ) + ( 5 ).( 3 ) |
| ( 0 ).( 4 ) + ( 3 ).( 5 ) |
( 1 ).( 4 ) + ( 4 ).( 5 ) |
( 2 ).( 4 ) + ( 5 ).( 5 ) |
O operador ## calcula o produto de uma matriz, multiplicando as linhas da primeira matriz pelas colunas da segunda. A segunda matriz deve ter o mesmo número de linhas que a primeira tem de colunas. A matriz resultante terá o número de linhas da primeira matriz e o mesmo número de colunas da segunda matriz.
Por exemplo:
IDL> print, a ## b
10 13
28 40Os cálculos são feitos desta forma:
| A 0,0 . B 0,0 + A 1,0 . B 0,1 + A 2,0 . B 0,2 | A 0,0 . B 1,0 + A 1,0 . B 1,1 + A 2,0 . B 1,2 |
| A 0,1 . B 0,0 + A 1,1 . B 0,1 + A 2,1 . B 0,2 | A 0,1 . |
Usando os valores atuais:
( 0 ).( 0 ) + ( 1 ).( 2 ) + ( 2 ).( 4 ) |
( 0 ).( 1 ) + ( 1 ).( 3 ) + ( 2 ).( 5 ) |
| ( 3 ).( 0 ) + ( 4 ).( 2 ) + ( 5 ).( 4 ) |
( 3 ).( 1 ) + ( 4 ).( 3 ) + ( 5 ).( 5 ) |
A função WHERE
A função WHERE avalia uma expressão e retorna um índice unidimensional de cada elemento em um vetor para todas as expressões verdadeiras (ele retorna a posição, não os valores dos dados). Se a expressão for falsa, o valor de retorno é -1. Por exemplo, iremos alterar todos os elementos entre 0.4 e 0.5 de uma matriz para 1.0:
IDL> x = findgen (360) *!dtor
IDL> data = sin(x)
IDL> indices = where ( data gt 0.4 and data lt 0.5, count)
IDL> print, count
12
IDL> data [indices] = 1.0Observe que na terceira linha, onde se encontra a função WHERE há um argumento chamado count, este argumento cria uma variável com o nome que você decidir (no exemplo ela é chamada de count), esta variável irá retornar o número total de elementos encontradas pela função.
Uma matriz multidimensional também pode utilizar a função WHERE. Por exemplo,
IDL> d = dist (100)
IDL> surface, d
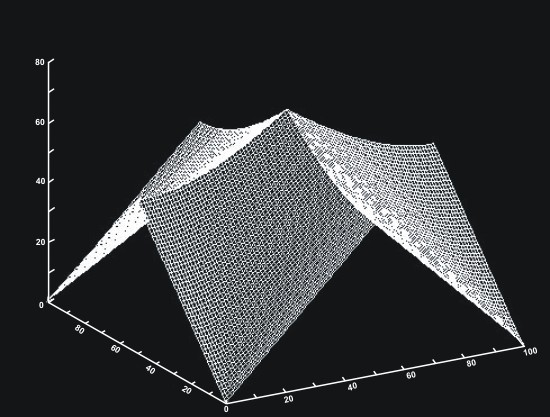
IDL> multi_ind = where (d gt 65, count)
IDL> print, count
145
IDL> d [multi_ind] = 0.0
IDL> surface, d
Note que os comandos são praticamente iguais, aos de uma matriz unidimensional.